问题定义
机器人
- n 个机器人
- 假设机器人是圆盘形,并且在二维平面内移动
- 机器人 A 具有以下外部状态(其他机器人可以观察到该属性)
:当前位置(圆盘中心) :圆盘半径(也可以理解为安全距离) :当前速度
- 机器人 A 具有以下内部状态(其他机器人无法观察到)
:机器人的最大速度 :首选速度(没有其他机器人挡路时会采用的速度)
目标
- 每个机器人独立为自己选择一个新的速度
,保证在预设的时间 T 内不会发生碰撞 - 机器人的新速度应尽可能接近
约束
机器人之间不得相互通信,只能对其他机器人的当前位置和速度进行观察
前置知识
VO: Velocity Obstacle
假设机器人 A 和机器人 B 在空间中相遇,各自的安全距离分别为
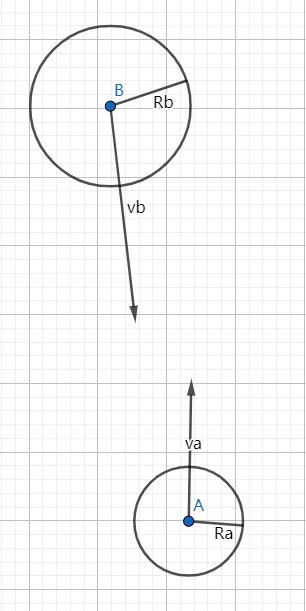
为了避免两个机器人发生碰撞,我们需要确保每一帧的移动,两个机器人之间的距离大于等于
如果我们以机器人 A 为参考系,将 A 看成一个静止的质点,那么 B
就是一个半径为
由于移动过程是连续的,且瞬时时刻的移动应该是从起始点到终点的一条直线,不能够直接穿过大圆到达大圆的正后方,因此大圆相对指点位置的后方的锥形区域也是不可达的(如下图的灰色区域所示)
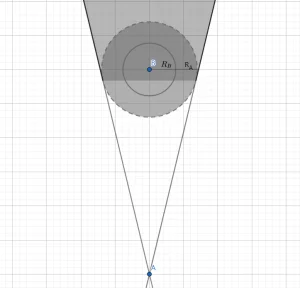
为了简化计算,VO 算法将整个三角形区域假定为潜在的碰撞区域,并需要进行规避。
刚才的讨论均基于笛卡尔坐标系进行。通过将该坐标系中的每个点除以时间变量 t,我们可以得到速度向量场。理论上,如果智能体 A 和 B 的相对速度向量位于红色三角形区域之外,那么它们就有足够的空间和时间来安全地避开对方,从而确保不会发生碰撞。
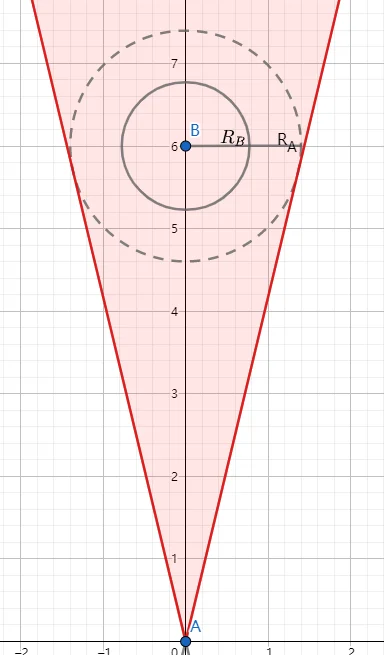
VO 存在的问题:抖动
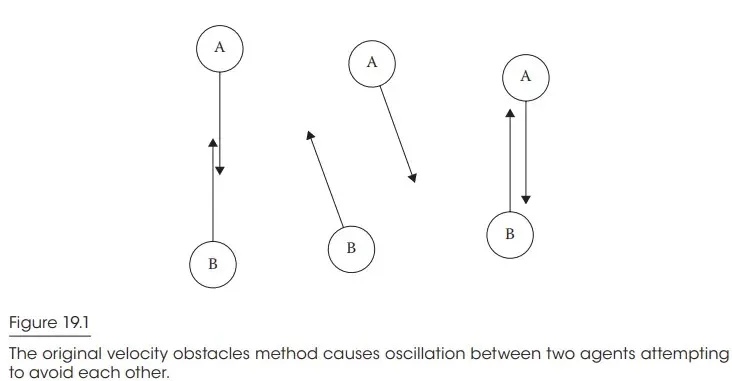
如果机器人A和机器人B均采用了VO算法并相互对向移动,根据VO算法的特性,它们将在错位和速度旋转之间不断切换,这可能导致它们出现不规律的振动现象。尽管这种情况可能不会导致最终的碰撞,但两个机器人的这种振动行为看起来缺乏流畅性,不够优雅。
VO 算法之所以容易引发抖动现象,主要是因为其核心假设是其他物体保持恒定速度稳定前进。
解决策略: RVO(Reciprocal Velocity Obstacle)
为了克服 VO 算法中出现的抖动问题,RVO 算法采取了一种更为灵活的策略。它假设其他智能体也会采用与我们相似的策略,而不是简单地保持匀速直线运动。
RVO
算法倡导的是一种相互协作的避障机制,即在遇到潜在碰撞时,双方都承担一半的责任,只将速度改变
ORCA(Optimal Reciprocal Collision Avoidance)
优势
相比于 RVO 算法,ORCA 算法将问题转化为线性规划问题来求解,这使得在多智能体系统中计算每个智能体的新速度变得更加高效。
在速度向量场上重新考虑碰撞问题
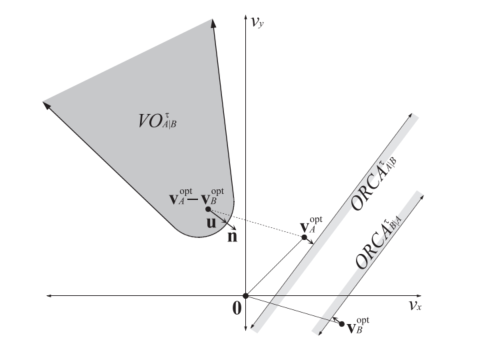
在图中,阴影部分表示可能发生碰撞的风险区域。该区域中的每一个点都代表一个速度矢量。如果机器人
A 和 B 的相对速度向量
为了实现避撞,A 和 B 可以沿着最快离开碰撞风险区域的方向调整自己的速度,并且各自承担一半的避障责任。以机器人 A 为例,我们可以从相对速度矢量开始,沿着指向阴影区域外的方向,计算出一个偏移量。在这个偏移量的基础上,我们可以构建一个垂直于该方向的法线。在避障决策中,法线的一侧将构成机器人 A 可以安全选择的速度空间,即机器人 A 可以在这个区域内自由选择速度矢量以避免碰撞。
考虑多智能体的情况
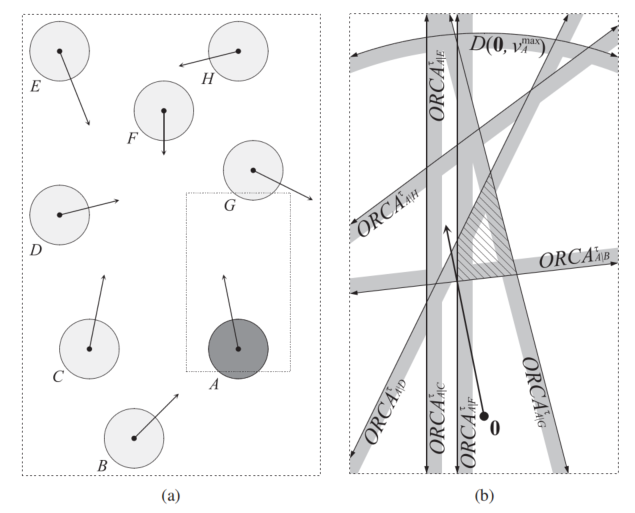
对机器人 A 进行策略规划,通过 ORCA 算法,我们可以确定每个邻近机器人相对于 A 的防撞半平面。利用线性规划,求解这些半平面的交集,如上图(b)所示的斜线阴影区域,便是机器人 A 可以安全移动的速度空间。简而言之,机器人 A 只需选择一个速度向量,使其落在这个斜线阴影区域内,即可有效避免与其他机器人的碰撞。
相比于求解复杂的弧线平面交集,线性规划问题在计算上更为高效,因为它简化了计算过程,减少了所需的计算量。这种方法不仅优化了求解时间,也提高了算法在实际应用中的可行性和效率。
参考文献
- https://indienova.com/indie-game-development/vo-rvo-orca/
- https://gamma.cs.unc.edu/ORCA/publications/ORCA.pdf